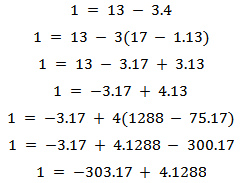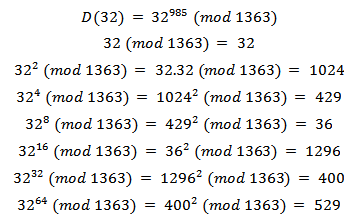Como codificar e decodificar uma palavra na sua HP utilizando o método de criptografia RSA

>Você já utilizou sua calculadora para efetuar cálculos de aritmética modular? É possível calcular potências com expoentes maiores que mil, em aritmética modular, em sua calculadora científica? A resposta para a segunda pergunta é sim. Esse artigo proporcionará ao leitor algum contato com as operações matemáticas envolvidas em um exemplo simples de codificação e decodificação utilizando o método RSA.

Primeiramente preciso falar que esse tópico com certeza foi um dos mais marcantes em meus estudos de matemática. Eu já havia lido sobre criptografia RSA no curso de Redes, porém havia sido uma abordagem puramente teórica e bastante abstrata. Até então não tinha achado nada de especial em criptografia. No curso de Matemática Discreta, comecei a enxergar com outros olhos a aritmética modular e as equações diofantinas lineares. Até que, após algumas reuniões e algumas conversas informais com alguns colegas e professores, resolvi pesquisar mais sobre o assunto e dei-me conta da relevância do tema. Acredito que possa existir alguma utilização de uma variante desse algoritmo em questões de segurança e acesso de pequenas aplicações. Além do mais, não é difícil encontrar por aí o porquê de existir tanto fascínio no método RSA: foi uma das grandes inovações em criptografia de chave pública, é considerado um dos métodos mais seguros já implementados e é fundamentado na teoria clássica dos números, além de ser amplamente utilizado na Internet. Assim, decidi divulgar o resultado dos meus estudos e compartilhar com os leitores dessa edição um exemplo prático de codificação e decodificação de uma palavra utilizando o método RSA de forma bem simples.

É importantíssimo notar que o leitor não encontrará no artigo provas matemáticas e muito menos definições teóricas, visto que para isso seria necessário no mínimo um curso completo de Matemática Discreta. Irei apenas transcrever o método de resolução de um dos exercícios que chamou a atenção de um grupo de estudantes que estava se preparando para uma prova final.

O Rivest-Shamir-Adleman (RSA) é um sistema de criptografia no qual, de acordo com Welsh (veja artigo na seção de Recursos), a segurança é fundamentada na crença de que não existe método rápido de fatorar números que resultam do produto entre dois números primos grandes. De acordo com o mesmo autor, os procedimentos de codificação e decodificação utilizando esse método são os seguintes:

1. Encontre dois números primos “grandes” p e q e defina n como sendo n = pq.
2. Encontre o “maior inteiro aleatório” d de tal forma que o inteiro d e o inteiro
3. (n) = (p – 1)(q – 1) sejam primos entre si.
4. Compute o único inteiro no intervalo 1 < = e < = O(n) pela fórmula ed = 1 (mod O(n)).
5. Torne conhecida a chave pública que consiste no par de inteiros (e, n).
6. Represente M, a mensagem a ser transmitida, como um inteiro no intervalo {1,…, n}; quebre M em blocos se M for muito grande.
7. Codifique o bloco num criptograma de acordo com a regra C(b) = b^e (mod n).
8. Decodifique o bloco codificado utilizando a chave privada d e a regra D(bc) = bc^d (mod n).

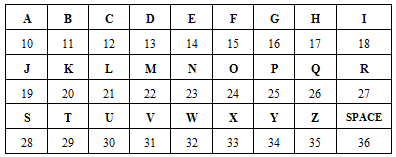
Antes de qualquer coisa, precisamos pré-codificar a palavra em uma sequência de números. Nesse pequeno exemplo, a palavra escolhida foi “OVOS” e a tabela de pré-codificação é a seguinte.

De acordo com a tabela, a letra “O” é representada pelo número 24, a letra “V” é representada pelo número 31 e a letra “S” é representada pelo número 28. Portanto a palavra “OVOS” é representada pela sequência 24312428.

Para quebrar a mensagem em blocos nesse exemplo, é necessário que os blocos sejam formados pelo maior número possível menor que n. Normalmente, p e q são números primos grandes formados por centenas de algarismos. Nesse exemplo simples, serão utilizados números pequenos. Os valores escolhidos para p e q são os números primos 29 e 47, respectivamente. n = pq n = 29.47 n = 1363 Assim, cada bloco precisa ser o maior número possível menor que 1363. Percorrendo a sequência 24312428 da esquerda para a direita, observa-se que o número 2431 é maior que n. Portanto o primeiro bloco será o número 243. A sequência restante é representada por 12428. Seguindo o raciocínio, 12428 é maior que 1363, logo o segundo bloco será o número 1242. O último bloco, finalmente, será formado pelo número 8. Nesse artigo, será executada a codificação e decodificação apenas do primeiro bloco. Os cálculos do segundo e do terceiro bloco ficam a cargo do leitor, caso haja interesse.

A chave codificadora é dada pela fórmula C(b) = b^e (mod n). Usando uma variante do algoritmo Euclidiano, o e escolhido é 17. Substituindo os parâmetros e e n obtém-se a fórmula: C(b) = b¹⁷ (mod 1363).

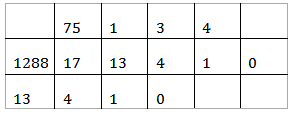
Substituindo p e q na seguinte fórmula O(n) = (p – 1)(q – 1), tem-se que O(n) = 1288. Para determinar d, faça o mdc(O(n), e). Para conferir, lembre-se da propriedade do inverso: d = e^-1 se ed (mod O(n) )= 1. Calculando o mdc entre 1288 e 17:

Portanto, o mdc entre 1288 e 17 é 1. Utilizando o esquema gráfico do mdc acima, é possível escrever o mdc entre 1288 e 17 na forma de combinação linear de 17 e 1288:
O número que multiplica o 17 é o -303. O d seria esse número. Porém como o expoente precisa ser positivo, deve-se somar -303 com 1288. Portanto, o valor de d é 985. Substituindo d e n, obtém-se a regra de decodificação. Portanto, a fórmula decodificadora é a seguinte: D(bc) = bc⁹⁸⁵ (mod 1363)

Tendo em mãos as regras de codificação e decodificação, o exercício prossegue com a aplicação da fórmula de codificação no primeiro bloco.

Logo, o primeiro bloco codificado é representado pelo número 32.

Note que para realizar os cálculos abaixo são necessários apenas lápis, borracha e calculadora científica. A sequência de cálculos abaixo mostra uma maneira de calcular 32 elevado à potência 985 módulo 1363.

Fazer essa última conta, 850755 (mod 1363), com uma calculadora científica em mãos é simples. Faça 850755/1363. Do resultado que aparecer no visor, subtraia a parte inteira. Se o resultado no visor for algo parecido com 624.1782832, subtraia 624 desse valor. Multiplique o resultado da subtração que apareceu no visor por 1363. O resultado será 243. Logo, 32⁹⁸⁵(mod 1363) = 243. O número encontrado é o valor esperado, ou seja, o valor do primeiro bloco. Caso o leitor tenha curiosidade, fique à vontade para codificar e decodificar o segundo e o terceiro bloco.

Fica assim compartilhado um método simples de efetuar o processo de codificação e decodificação seguindo o método RSA. Também está provado que com uma calculadora na mão, é perfeitamente possível fazer potenciações em aritmética modular com tranquilidade, mesmo que o expoente não seja tão pequeno. Se mais alguém além de mim e de meus colegas de estudo criar interesse pelo assunto, tenho certeza que o objetivo deste artigo terá sido atingido.

WELSH, Dominic. (1988) Codes and Cryptography. Oxford University Press, New York.
RSA na Wikipedia: http://en.wikipedia.org/wiki/RSA

»Esta é uma publicação eletrônica da Sociedade Brasileira de Computação ? SBC. Qualquer opinião pessoal não pode ser atribuída como da SBC. A responsabilidade sobre o seu conteúdo e a sua autoria é inteiramente dos autores de cada artigo.